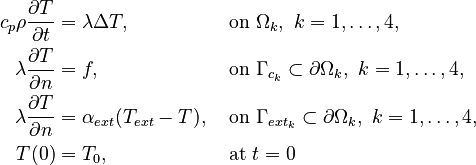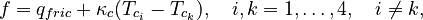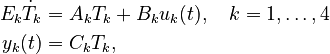Simplified machine tool

Simplified machine tool

Background
Benchmark ID	Coarse: simplifiedMachineToolCoarseSA1_n28183m6q5 simplifiedMachineToolCoarseSA2_n10080m8q8 simplifiedMachineToolCoarseSA3_n3721m8q8 simplifiedMachineToolCoarseSA4_n3276m5q5 Fine: simplifiedMachineToolFineSA1_n106641m6q5 simplifiedMachineToolFineSA2_n35408m8q8 simplifiedMachineToolFineSA3_n11956m8q8 simplifiedMachineToolFineSA4_n12812m5q5
Category	CRC-TR-96
System-Class	LTI-FOS
Parameters
nstates	Coarse: 28183 10080 3721 3276 Fine: 106641 35408 11956 12812
ninputs	6 8 8 5
noutputs	5 8 8 5
nparameters	0
components	A, B, C, E
Copyright
License	Creative Commons Attribution 4.0 International
Creator	CRC/TR 96: Stefan Sauerzapf Andreas Naumann Julia Vettermann Jens Saak
Editor	Julia Vettermann
Location
https://doi.org/10.5281/zenodo.10017861

1 Motivation

Due to the increasing interest in manufacturing accuracy without an additional energy demand for cooling, knowledge about the thermo-elastic behavior of entire machine tools becomes crucial. Methods to correct the thermally induced position error between the tool-center-point (TCP) and the workpiece in real-time are needed. Therefore, reduced-order models that enable a fast simulation of entire machine tools are applied in the design and production process.

2 Description

Figure 1: Subassemblies of the simplified machine tool.

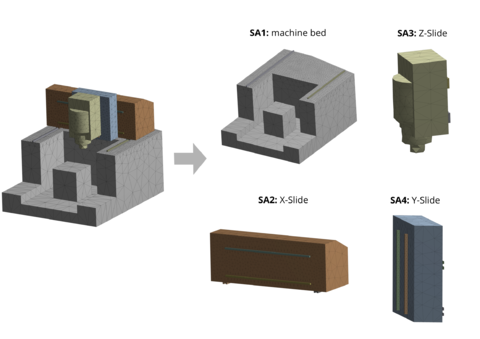
The simplified machine tool benchmark is a linear time-invariant thermal model used for investigation and demonstration purposes in the CRC/TR 96. For more information on first numerical experiments, see . It is divided into four stationary subassemblies (SA): machine bed, X-slide, Z-slide, Y-slide, see Fig. 1. The thermal finite element (FE) model was generated in ANSYS and afterwards the FE system matrices were exported for post-processing, such as MOR, to MATLAB. The interaction between the subassemblies is modeled by contact boundary conditions. In this case an input-output coupling was used, i.e., the model is block diagonal and thus the subassemly models can be reduced separately for structure preserving MOR. The evolution of the temperature field is modeled by the heat equation

$\begin{align} c_p\rho\frac{\partial T}{\partial t}&=\lambda \Delta T, & &\text{ on } \Omega_k , \text{ } k=1,\dots,4, \\ \lambda\frac{\partial T}{\partial n}&=f, & &\text{ on } \Gamma_{c_k} \subset\partial\Omega_k , \text{ } k=1,\dots,4, \\ \lambda\frac{\partial T}{\partial n}&=\alpha_{ext}(T_{ext}-T), & &\text{ on } \Gamma_{ext_k} \subset\partial\Omega_k , \text{ } k=1,\dots,4, \\ T(0)&=T_0, & &\text{ at } t=0 \end{align}$

with

$\begin{align} f=q_{fric}+\kappa_c(T_{c_i}-T_{c_k}), \quad i,k=1,\dots,4, \quad i\neq k, \end{align}$

and

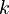
$k$	- number of the subassembly, $k=1,\dots, 4$
$T$	- temperature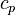
$c_p$	- specific heat capacity
$\rho$	- density
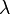
$\lambda$	- heat conductivity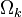
$\Omega_k$	- domain of the k-th subassembly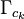
$\Gamma_{c_k}$	- contact boundary of the k-th subassembly (partly time varying, moves with the position of the z-slide (considered as heat flow))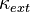
$\kappa_{ext}$	- heat transfer coefficient between a subassembly and the ambient air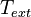
$T_{ext}$	- external temperature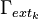
$\Gamma_{ext_k}$	- contact boundary with the ambience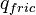
$q_{fric}$	- friction driven heat flow induced by the movement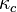
$\kappa_c$	- heat transfer coefficient between two subassemblies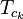
$T_{c_k}$	- temperature of the contact area of subassembly k.

The finite element discretization of the heat conduction models leads to the four systems

$\begin{align} E_k\dot{T}_k&=A_kT_k + B_k u_k(t),\quad k=1,\dots,4\\ y_k(t)&=C_k T_k,\\ \end{align}$

with

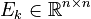
$E_k \in \mathbb{R}^{n\times n}$	- capacity matrix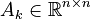
$A_k \in \mathbb{R}^{n\times n}$	- conductivity matrix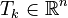
$T_k \in \mathbb{R}^n$	- discrete temperature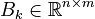
$B_k \in \mathbb{R}^{n \times m}$	- input map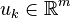
$u_k \in \mathbb{R}^m$	- input vector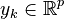
$y_k \in \mathbb{R}^p$	- output vector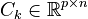
$C_k \in \mathbb{R}^{p \times n}$	- output map.

3 Data

The system matrices can be downloaded from zenodo. There is a set of matrices for each subassembly. The numbering of the subassemblies is shown in Fig. 1. The model is available in two versions: a fine discretization with 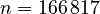$n=166\,817$ degrees of freedom and a coarse discretization with an overall system dimension of 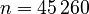$n=45\,260$. The dimensions of the subassemblies of both models can be seen in the following table:

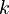
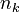
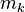
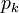
Model	Subassembly $k$	$n_k$	$m_k$	$p_k$
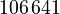
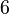
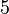
fine	1	$106\,641$	$6$	$5$
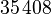
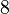
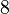
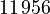
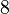
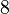
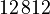
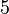
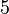
	2	$35\,408$	$8$	$8$
	3	$11\,956$	$8$	$8$
	4	$12\,812$	$5$	$5$
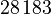
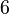
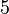
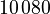
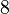
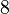
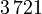
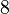
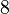
coarse	1	$28\,183$	$6$	$5$
	2	$10\,080$	$8$	$8$
	3	$3\,721$	$8$	$8$
	4	$3\,276$	$5$	$5$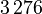

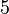
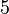
4 Origin

The simplified machine tool model was developed in the CRC/TR 96 Project-ID 174223256 financed by the German Research Foundation DFG.

5 Citation

To cite this benchmark, use the following references:

• For the benchmark itself and its data:

 @misc{dataSauNVetal23,
   author = {S. Sauerzapf and A. Naumann and J. Vettermann and J. Saak},
   title = {Matrices for a simplified machine tool model},
   howpublished = {hosted at {MORwiki} -- Model Order Reduction Wiki},
   year = 2023,
   doi = {10.5281/zenodo.10017861}
 }

• For the background on the benchmark:

 @inproceedings{SauVNetal20,
   author = {Sauerzapf, S. and Vettermann, J. and Naumann, A. and Saak, J. and Beitelschmidt, M. and Benner, P.},
   title = {Simulation of the thermal behavior of machine tools for efficient machine development and 
             online correction of the {Tool} {Center} {Point} ({TCP})-displacement},
   booktitle = {Conference Proceedings on Thermal Issues, Aachen, 26-27 February},
   organization = {euspen},
   pages = {135--138},  
   year = {2020},
   url = {https://www.euspen.eu/knowledge-base/TI20125.pdf }
 }

7 Contact

Jens Saak