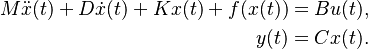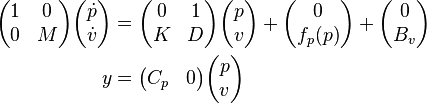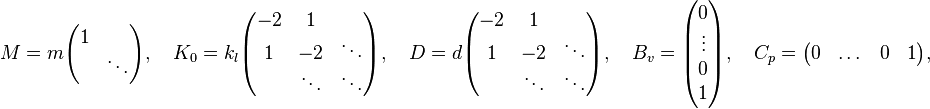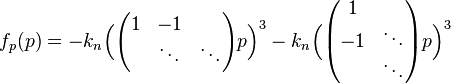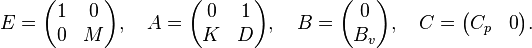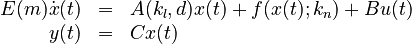Note: This page has not been verified by our editors.
Note: This page has not been verified by our editors.
Description: Mass-Spring-Damper System
This benchmark is a generalization of the nonlinear mass-spring-damper system presented in [1], which is concerned with modeling the a mechanical systems consisting of chained masses, linear and nonlinear springs, and dampers. The underlying mathematical model is a second order system:
First Order Representation
The second order system can be represented as a first order system as follows:
with the components:
and the nonlinear term:
and thus yielding the classic first order components:
The parameters for the mass 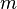 , linear spring constant
, linear spring constant 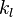 , nonlinear spring constant
, nonlinear spring constant 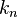 , and damping
, and damping 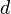 are chosen in [1] as
are chosen in [1] as 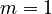 ,
, 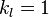 ,
, 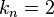 , and
, and 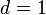 .
.
Data
The following Matlab code assembles the above described  ,
,  ,
,  and
and  parameter dependent matrices and the function
parameter dependent matrices and the function 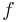 for a given number of subsystems
for a given number of subsystems  .
.
function [E,A,B,C,f] = msd(N)
U = speye(N); % Sparse unit matrix
T = gallery('tridiag',N,-1,2,-1); % Sparse tridiagonal matrix
H = gallery('tridiag',N,-1,1,0); % Sparse transport matrix
Z = sparse(N,N); % Sparse all zero matrix
z = sparse(N,1); % Sparse all zero vector
E = @(m) [U,Z;Z,m*U]; % Handle to parametric E matrix
A = @(kl,d) [Z,U;kl*T,d*T]; % Handle to parametric A matrix
B = sparse(2*N,1,1,2*N,1);
C = sparse(N,1,1,2*N,1);
f = @(x,kn) [z;-kn*( (H'*x(N+1:end)).^3 - (H*x(N+1:end)).^3)];
end
Dimensions
System structure:
System dimensions:
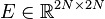 ,
,
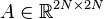 ,
,
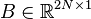 ,
,
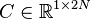 .
.
Citation
To cite this benchmark, use the following references:
- For the benchmark itself and its data:
- The MORwiki Community, Mass-Spring-Damper System. MORwiki - Model Order Reduction Wiki, 2018. http://modelreduction.org/index.php/Mass-Spring-Damper
@MISC{morwiki_msd,
author = {{The MORwiki Community}},
title = {Mass-Spring-Damper System},
howpublished = {hosted at {MORwiki} -- Model Order Reduction Wiki},
url = {https://modelreduction.org/morwiki/Mass-Spring-Damper},
year = 2018
}
- For the background on the benchmark:
@INPROCEEDINGS{morKawS15,
title = {Model Reduction by Generalized Differential Balancing},
author = {Y. Kawano and J.M.A. Scherpen},
booktitle = {Mathematical Control Theory I: Nonlinear and Hybrid Control Systems},
series = {Lecture Notes in Control and Information Sciences},
volume = {461},
pages = {349--362},
year = {2015},
doi = {10.1007/978-3-319-20988-3}
}
References
- ↑ 1.0 1.1 Y. Kawano and J.M.A. Scherpen, Model Reduction by Generalized Differential Balancing, In: Mathematical Control Theory I: Nonlinear and Hybrid Control Systems, Lecture Notes in Control and Information Sciences 461: 349--362, 2015.