Machine tool with relative movements

Note: This page has not been verified by our editors.

Machine tool with relative movements

Background
Benchmark ID	rail_n91181m89q89 slider_n74392m8q8
Category	CRC-TR-96
System-Class	LTI-FOS
Parameters
nstates	91181 74392
ninputs	89 8
noutputs	89 8
nparameters	0
components	A, B, C, E
Copyright
License	Creative Commons Attribution 4.0 International
Creator	CRC/TR 96: Quirin Aumann Jens Saak Julia Vettermann
Editor	Julia Vettermann
Location
https://zenodo.org/records/8099979

Figure 1: Sketch of the geometry and the boundary conditions.

Description

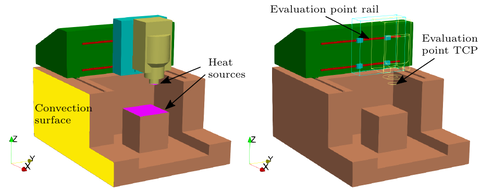
This benchmark models a machine tool composed out of two components. The "rail" part is the machine bed with a guide rail, the "slider" part moves along the rail on four carts and carries the tool. Slider and rail move relative to each other during the simulated work process. This relative movement is realized by decomposing a weighting function into a Fourier series and superposing their weighted sum, which depends on the current position of the slider. The weighted sums are then used in every time step to compute the thermal load exchanged between the two components. This approach is described in more detail in. Due this approach, additional inputs and outputs are created, but the resulting system is still LTI, despite the relative movement.

Figure 2: Temperature evaluation on the rail midpoint.

Figure 3: Temperature evaluation on the TCP.

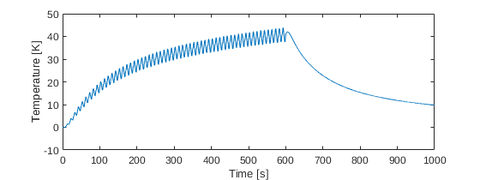
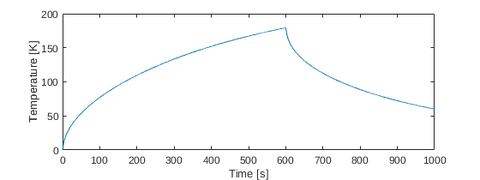
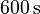The thermal response of the system has been investigated in. Here, the temperature change in the middle of the rail and the tool center point (TCP), respectively, have been measured during a simulated work process. In the first $600\,\mathrm{s}$, the slider is moving from left to right constantly. Afterwards, the slider remains at its location. During the first $600\,\mathrm{s}$ six heat sources introduce energy into the system. They are located at the TCP, the work piece, and the four carts (see Fig. 1). After the slider stops to move, the heat sources are switched off. The temperature evaluations are given in Figs. 2 and 3.

Dimensions

Both systems have the same structure:

$\begin{align} E \dot{x}(t) &= A x(t) + B u(t), \\ y(t) &= C x(t) \end{align}$

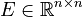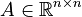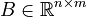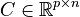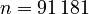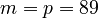System dimensions: $E \in \mathbb{R}^{n \times n}$, $A \in \mathbb{R}^{n \times n}$, $B \in \mathbb{R}^{n \times m}$, $C \in \mathbb{R}^{p \times n}$, with $n=91\,181$, $m=p=89$ for the rail system and 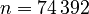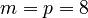$n=74\,392$, $m=p=8$ for the slider system.

Data

The data is available at Zenodo.

Remarks

• The dataset contains also the data for the movement profile that was used to produce the results reported here. This can be changed by modifying the variable sc.
• The system also contains the elastic degrees of freedom and their coupling in $x$-direction.

Origin

The Machine tool with relative movements model was developed in the CRC/TR 96 Project-ID 174223256 financed by the German Research Foundation DFG.

Citation

To cite this benchmark, use the following references:

• For the benchmark itself and its data:

 @misc{dataAumSV23,
   author =       {Q. Aumann and J. Saak and J. Vettermann},
   title =        {Model of a machine tool with relative movements},
   howpublished = {hosted at {MORwiki} -- Model Order Reduction Wiki},
   year =         2023,
   doi =          {10.5281/zenodo.8099979}
 }

• For the background on the benchmark:

 @article{AumBSetal23,
   author    = {Q. Aumann and P. Benner and J. Saak and J. Vettermann},
   booktitle = {Lecture Notes in Production Engineering},
   publisher = {Springer International Publishing},
   title     = {Model order reduction strategies for the computation of compact machine tool models},
   year      = {2023},
   editor    = {S. Ihlenfeldt},
   pages     = {132--145},
   doi       = {10.1007/978-3-031-34486-2_10},
 }