Low-Pass Butterworth Filter

Description

This benchmark from represents an analogue low-pass Butterworth filter. A Butterworth filter is an electrical signal processing filter. The low-pass variant allows signals with frequencies below a cut-off frequency 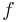$f$ to pass and mitigates those with frequencies above $f$.

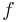Data

The following Matlab code assembles the above described $A$, $B$ and $C$ matrix for a given state-space dimension $N$ and a cut-off frequency $f=1 rad/s$.

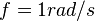[A,B,C,D] = butter(N,1,'low','s'); % D = 0

The butter method is part of the Control System Toolbox; an example for $N=100$ is provided here: File:Lpbw mat.zip

Dimensions

System structure:

$\begin{align} \dot{x}(t) &= Ax(t) + Bu(t) \\ y(t) &= Cx(t) \end{align}$

System dimensions:

$A \in \mathbb{R}^{N \times N}$, $B \in \mathbb{R}^{N \times 1}$, $C \in \mathbb{R}^{1 \times N}$.

Citation

To cite this benchmark, use the following references:

• For the benchmark itself and its data:

The MORwiki Community, Low-Pass Butterworth Filter. MORwiki - Model Order Reduction Wiki, 2018. http://modelreduction.org/index.php/Low-Pass_Butterworth_Filter

@MISC{morwiki_lpbw,
  author =       {{The MORwiki Community}},
  title =        {Low-Pass Butterworth Filter},
  howpublished = {{MORwiki} -- Model Order Reduction Wiki},
  url =          {https://modelreduction.org/morwiki/Low-Pass_Butterworth_Filter},
  year =         {2018}
}

• For the background on the benchmark:

@ARTICLE{morAntSS01,
  author =       {A.C. Antoulas and D.C. Sorensen and S. Gugercin},
  title =        {A Survey of Model Reduction Methods for Large-Scale Systems},
  journal =      {Contemporary Mathematics},
  volume =       {280},
  pages =        {193--219},
  year =         {2001},
  url =          {http://www.ams.org/books/conm/280/4630}
}

Contact

Christian Himpe