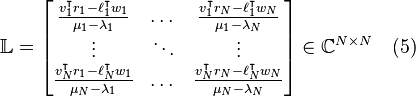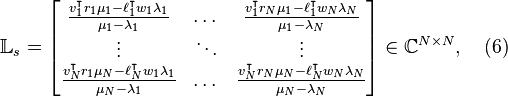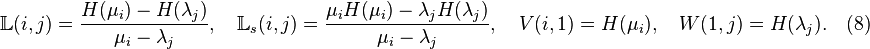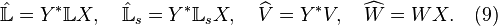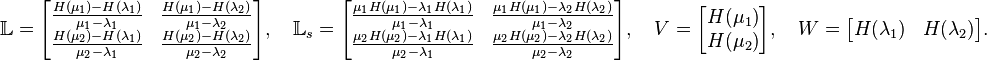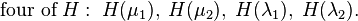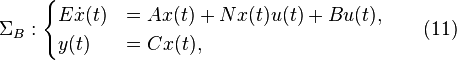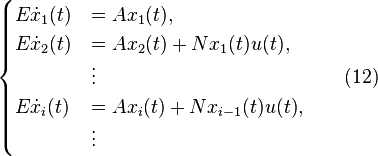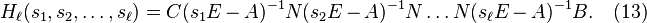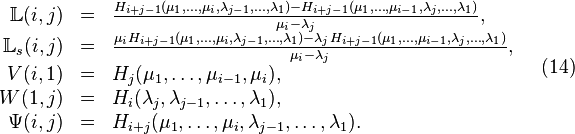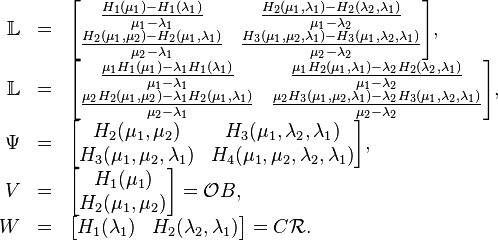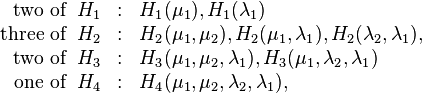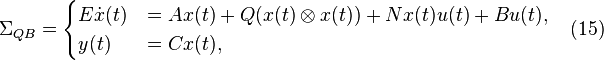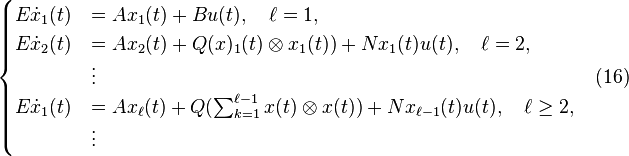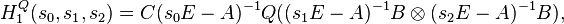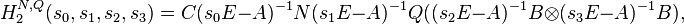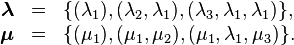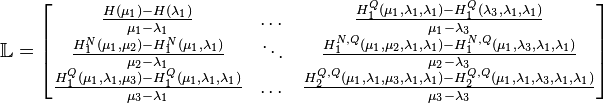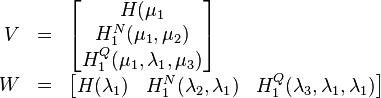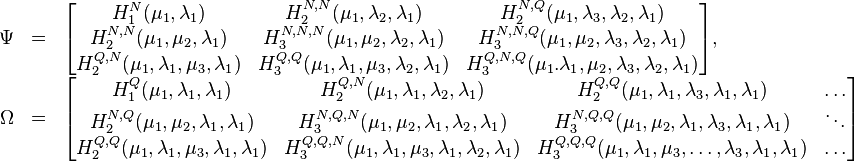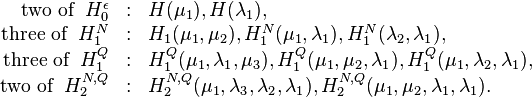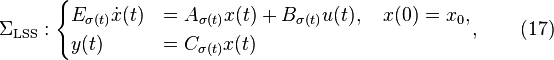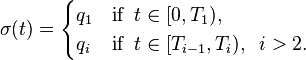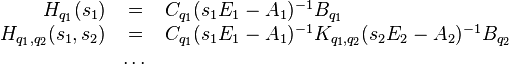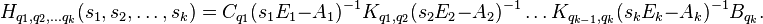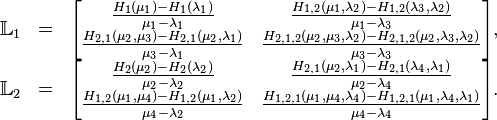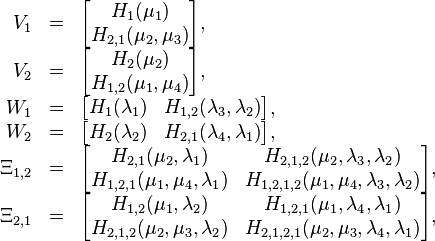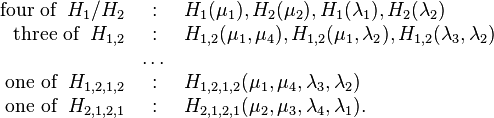Note: This page has not been verified by our editors.
Note: This page has not been verified by our editors.
The Loewner Framework is a frequency-domain system identification, system realization and model reduction method, named after Charles Loewner, who introduced the Loewner Matrix which is essential to this method based on ideas from [1].
Introduction
Model order reduction is commonly used to simulate and control complex physical processes. This is done by replacing the large-scale system model described in terms of differential equations by a system of much lower dimension that has similar response characteristics. In many situations, a model (the collection of differential equations written in matrix format) for the underlying dynamical process is not explicitly available. Hence, the system matrix realization can not be directly obtained. Instead, a black box is provided that produces input-output measurements. These situations include VLSI modeling from chips or real time simulation of multi-body dynamics with constraints.
We study reduction methods based on moment matching, that is, matching of the coefficients of power series expansions of the transfer function at selected points in the complex plane. More precisely, values of the underlying transfer function, together with the values of its derivatives are interpolated. Hence, the main underlying problem is rational interpolation. Different methods based on Krylov iteration, as well as the Arnoldi or the Lanczos procedures, and multi-point (rational) versions thereof.
Interpolatory model reduction methods compute ROMs (reduced order models) by means of interpolating the response of the original system at selected points (usually the transfer function). The Loewner framework (introduced in [2]) falls into this category. It is a data-driven method that directly constructs a ROM using only measured data (samples of the transfer function). Additionally, by compressing the (usually large) data set, it extracts the dominant features and eliminates the inherent redundancies. For a recent survey on the Loewner framework for linear systems, see [3]. For the nonlinear case, this method requires appropriate definition of transfer functions, but the main procedure does not differ too much from the one applied for the linear case. Some of the extensions include the bilinear systems case in [4], quadratic-bilinear systems [5] and linear switched systems [6]. The dissertation [7] represents a comprehensive collection of these methods.
The motivation behind developing generalized versions of the Loewner framework to new systems is that such classes of systems can be viewed as a bridge between linear and nonlinear systems. For example, one can always write an approximation of a nonlinear system by means of a bilinear system (Carleman linearization [8]). Furthermore, for certain types of nonlinear systems, one can always find an equivalent quadratic-bilinear model without performing any approximation (McCormick relaxation [9]) whatsoever. Linear switched systems can be viewed as a special class of hybrid systems that are used to model coupled or distributed processes characterized by both discrete and continuous dynamics.
Loewner Framework for Linear Systems
We analyze linear time-invariant continuous-time systems described by the following equations:
where 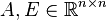 ,
, 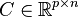 ,
, 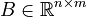 ,
, 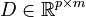 and
and 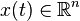 ,
, 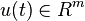 ,
, 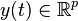 are state, input and output vector respectively.
The transfer function corresponding to
are state, input and output vector respectively.
The transfer function corresponding to 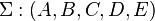 is computed as
is computed as 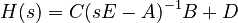 .
.
The Loewner framework can construct a reduced-order system by means of measured data.
In this context, data represent sample values of the underlying transfer function 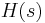 at selected interpolation points (in some cases on the imaginary axis, when approximating the frequency response of the original system).
A Loewner matrix pencil
at selected interpolation points (in some cases on the imaginary axis, when approximating the frequency response of the original system).
A Loewner matrix pencil 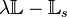 is composed of the Loewner matrix
is composed of the Loewner matrix 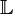 and the shifted Loewner matrix
and the shifted Loewner matrix 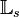 .
This pencil represents a surrogate of the original matrix pencil
.
This pencil represents a surrogate of the original matrix pencil 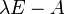 .
.
The Loewner framework originates from rational approximation theory (see [2][3]) and can be used to recover or reduce the original dynamical system by means of interpolating the transfer function.
For simplicity, assume that the data set contains an even number of measurements denoted with 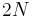 .
The next step is to partition the data measurements set into two disjoint data subsets, i.e. the left subset and the right subset as described in the following
.
The next step is to partition the data measurements set into two disjoint data subsets, i.e. the left subset and the right subset as described in the following
- Left set:
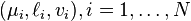 , Right set:
, Right set: 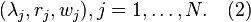
More precisely, the data in (2) is composed of  left interpolation points:
left interpolation points: 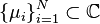 ,
,  left sample values:
left sample values: 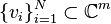 and
and  left tangential directions:
left tangential directions: 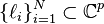 .
Additionally, we have
.
Additionally, we have  distinct right interpolation points:
distinct right interpolation points: 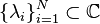 with
with  right sample values:
right sample values: 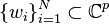 and right tangential directions:
and right tangential directions: 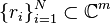 .
We seek a linear system
.
We seek a linear system 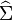 such that the associated transfer function
such that the associated transfer function 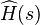 is a tangential interpolant to the original one,
is a tangential interpolant to the original one, 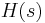 .
More precisely, the following interpolation conditions should then hold:
.
More precisely, the following interpolation conditions should then hold:
Next, arrange the measured data into matrix format as follows
The Loewner matrix is constructed in the following way
and is the solution of the following Sylvester equation 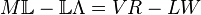 .
The shifted Loewner matrix can be constructed in the following way:
.
The shifted Loewner matrix can be constructed in the following way:
and is the solution of the following Sylvester equation 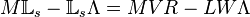 .
After rearranging the data into matrix format, we construct with basically no computational cost a Loewner linear model described by the following matrices
.
After rearranging the data into matrix format, we construct with basically no computational cost a Loewner linear model described by the following matrices
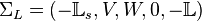 .
.
The 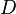 term does not play an important role in the Loewner framework since it is incorporated in the Loewner matrix
term does not play an important role in the Loewner framework since it is incorporated in the Loewner matrix 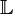 (see [2]).
Consequently, this term is taken to be
(see [2]).
Consequently, this term is taken to be 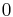 in (7).
Note that, in the SISO case we consider only one input and one output
in (7).
Note that, in the SISO case we consider only one input and one output 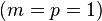 .
Then one can take
.
Then one can take ![R = L^\intercal = [1 \; 1 \; \dots \; 1] \in \mathbb{R}^N](/morwiki/images/math/c/b/7/cb7558fee0666baa84ab32c6e19f3cd9.png) and explicitly write
and explicitly write
The Loewner model can completely recover the dynamics of the original system if enough measurements are provided. We can hence distinguish two cases:
- The right amount of data is available - in this case one can exactly recover the original system;
- A redundant amount of data is provided - in this case one can approximate the original system.
In the first case, the matrix pencil 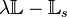 is regular.
Then, the transfer function of the Loewner model can be computed as follows
is regular.
Then, the transfer function of the Loewner model can be computed as follows 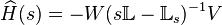 .
This situation is encountered when the number of measurements is enough to recover the original system (one would require exactly
.
This situation is encountered when the number of measurements is enough to recover the original system (one would require exactly 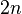 measurements to recover a system of order
measurements to recover a system of order  ).
In the second case, the pencil
).
In the second case, the pencil 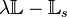 is singular.
Then, the definition of the transfer function can be adapted as in [10], i.e.
is singular.
Then, the definition of the transfer function can be adapted as in [10], i.e. 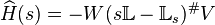 .
Here, the
.
Here, the 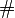 operator represents the Moore-Penrose or Drazin generalized inverse.
In real world applications, the reason behind the singularity of the matrix pencil
operator represents the Moore-Penrose or Drazin generalized inverse.
In real world applications, the reason behind the singularity of the matrix pencil 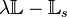 is the overfitting of the data that contains in most cases redundant or inaccurate measurements.
is the overfitting of the data that contains in most cases redundant or inaccurate measurements.
We focus on the second case, which is more relevant in practice.
In this case, since the Loewner pencil is singular, we can use the singular value decomposition (SVD) to compress the data.
The truncation order  can be chosen by inspecting the singular value decay of the data.
Deciding on a specific value of
can be chosen by inspecting the singular value decay of the data.
Deciding on a specific value of  is usually done by making a trade-off between reduced-order model dimension and accuracy of fit.
Consider the SVD of the Loewner matrix
is usually done by making a trade-off between reduced-order model dimension and accuracy of fit.
Consider the SVD of the Loewner matrix 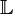 as
as 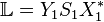 where
where 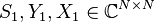 .
The singular values are nonnegative real scalars that give information on the numerical rank of matrices and are stored on the main diagonal of matrix
.
The singular values are nonnegative real scalars that give information on the numerical rank of matrices and are stored on the main diagonal of matrix 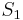 , as
, as 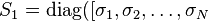 with
with 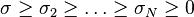 .
the matrices
.
the matrices 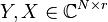 are obtained by selecting the first
are obtained by selecting the first  columns of the matrices
columns of the matrices 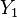 and
and 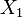 , respectively.
The reduced Loewner system is constructed by projecting the matrices
, respectively.
The reduced Loewner system is constructed by projecting the matrices 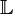 ,
, 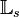 ,
,  ,
, 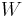 with
with 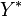 and
and 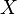 to the left and respectively, to the right, as
to the left and respectively, to the right, as
The dimension  of the the reduced system is typically chosen as follows; first set a tolerance value
of the the reduced system is typically chosen as follows; first set a tolerance value 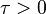 and then select the truncation order
and then select the truncation order  as the maximum number of normalized singular values that are larger than
as the maximum number of normalized singular values that are larger than 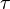 .
More precisely,
.
More precisely,  for
for 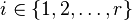 .
The projected Loewner model is given by
.
The projected Loewner model is given by
Given the SISO linear system as in (1), consider the tuples of left and right interpolation points: ![[\mu_1,\mu_2], [\lambda_1,\lambda_2]](/morwiki/images/math/c/e/1/ce1a96362e193cb1776452d2d0f4ad75.png) .
The recovered matrices can be written in terms of data samples in the following way:
.
The recovered matrices can be written in terms of data samples in the following way:
This reduced system matches 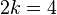 , for
, for 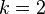 moments of the original system, namely:
moments of the original system, namely:
Loewner Framework for Bilinear Systems
Next, we turn our attention to bilinear systems 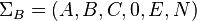 characterized by equations:
characterized by equations:
where 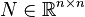 and the other quantities are exactly as in (1).
For simplicity of exposition, we will assume single-input and single-output scenarios (so
and the other quantities are exactly as in (1).
For simplicity of exposition, we will assume single-input and single-output scenarios (so 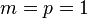 ) and that the
) and that the 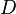 term is incorporated into the
term is incorporated into the  matrix (so
matrix (so 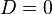 ).
Bilinear systems can be equivalently rewritten as an infinite set of systems of the form:
).
Bilinear systems can be equivalently rewritten as an infinite set of systems of the form:
The external representation of the bilinear system 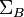 can be expressed in terms of Volterra series, which describe the nonlinear mapping of admissible inputs
can be expressed in terms of Volterra series, which describe the nonlinear mapping of admissible inputs  to the output
to the output 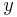 .
The solution of (11) can be written as
.
The solution of (11) can be written as 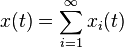 .
By considering
.
By considering 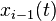 as a pseudo-input for the
as a pseudo-input for the  th equation in (12),
the frequency-domain behavior is described by a series of generalized transfer functions obtained by taking the multivariate Laplace transform of the degree
th equation in (12),
the frequency-domain behavior is described by a series of generalized transfer functions obtained by taking the multivariate Laplace transform of the degree  regular kernel.
More specifically, introduce the generalized multivariate transfer functions of system
regular kernel.
More specifically, introduce the generalized multivariate transfer functions of system 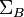 , as follows (for
, as follows (for 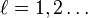 )
)
The explicit derivation of these types of transfer functions is based on the so-called Volterra series representation. The characterization of bilinear systems by means of rational functions suggests that reduction of such systems can be performed by means of interpolatory methods, i.e. by extending the Loewner framework.
Let 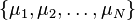 and
and 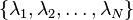 be two set of left and respectively, right interpolation
points in the complex plane.
Using samples of transfer functions in (13) evaluated at these points, we put together a realization of an order
be two set of left and respectively, right interpolation
points in the complex plane.
Using samples of transfer functions in (13) evaluated at these points, we put together a realization of an order  bilinear system.
The main property is that this reduced system matches those original samples.
Hence, for
bilinear system.
The main property is that this reduced system matches those original samples.
Hence, for 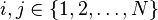 , one can explicitly write
, one can explicitly write
Given a SISO bilinear system as in (11), consider the ordered tuples of left and right interpolation points: ![[\{\mu_1\}, \{\mu_1,\mu_2\}],[\{\lambda_1\},\{\lambda_1,\lambda_2\}]](/morwiki/images/math/4/3/1/431b55218f38d374627aace60163f762.png) .
The recovered matrices can be written in terms of data samples in the following way:
.
The recovered matrices can be written in terms of data samples in the following way:
This reduced system matches eight moments of the original system, namely:
i.e. in total 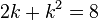 , for
, for 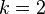 , moments are matched using this procedure.
, moments are matched using this procedure.
Loewner Framework for Quadratic-Bilinear Systems
Consider quadratic-bilinear systems 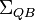 characterized by the following equations:
characterized by the following equations:
where 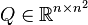 and the other quantities are exactly as in (1) and (11) for the SISO case (
and the other quantities are exactly as in (1) and (11) for the SISO case (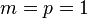 ).
The multi-input case is technically more involved but it is based on the same ideas.
It follows that the differential equation in (15) can be split into an infinite series of equations:
).
The multi-input case is technically more involved but it is based on the same ideas.
It follows that the differential equation in (15) can be split into an infinite series of equations:
Assume zero initial conditions and integrate both sides of the differential equations in (16).
By using the second equation in (15), we can find a closed form relation between the output  and the input
and the input  in terms of infinitely many multivariate time domain kernels.
Again, by transforming these functions to the frequency domain, we are able to construct rational multivariate transfer functions.
Some of these will be used in the proposed procedure.
More precisely, the one corresponding to level zero is the linear transfer function
in terms of infinitely many multivariate time domain kernels.
Again, by transforming these functions to the frequency domain, we are able to construct rational multivariate transfer functions.
Some of these will be used in the proposed procedure.
More precisely, the one corresponding to level zero is the linear transfer function 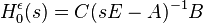 , which can also be denoted with
, which can also be denoted with 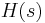 .
Furthermore, the two functions corresponding to level one are written as
.
Furthermore, the two functions corresponding to level one are written as 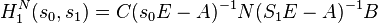 and
and
For the second level, proceed with the following example
In total, we can write 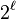 functions for each level
functions for each level 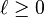 , as explicitly presented in [5].
Given a SISO quadratic-bilinear system
, as explicitly presented in [5].
Given a SISO quadratic-bilinear system 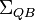 as in (15), choose
as in (15), choose 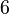 interpolation points
interpolation points 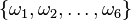 .
First partition this set into two disjoint sets corresponding to right and left points, as
.
First partition this set into two disjoint sets corresponding to right and left points, as 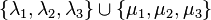 .
Next, consider the multi-tuples
.
Next, consider the multi-tuples 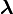 and
and 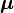 , composed of the tuples
, composed of the tuples
The Loewner matrix 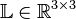 is a divided difference matrix, which is written as,
is a divided difference matrix, which is written as,
Similarly, the shifted Loewner matrix 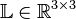 is computed; also the vectors
is computed; also the vectors  and
and 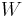
Next, construct the matrices 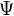 and
and  , corresponding to the bilinear and quadratic dynamics,
, corresponding to the bilinear and quadratic dynamics,
The matrix 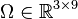 represents the reduced
represents the reduced  matrix.
It follows that given the system
matrix.
It follows that given the system 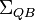 a reduced system
a reduced system 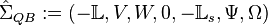 of order
of order 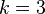 can be constructed.
This reduced system matches at most
can be constructed.
This reduced system matches at most 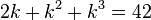 moments of the original system, i.e.
moments of the original system, i.e.
Loewner Framework for Linear Switched Systems
A continuous time linear switched system (LSS) is a dynamical system described by equations
where 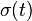 is the switching signal (
is the switching signal (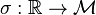 ),
),
 is the input,
is the input,  is the state,
is the state, 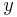 is the output, and
is the output, and 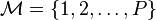 ,
, 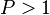 , is the set of discrete modes.
The system matrices
, is the set of discrete modes.
The system matrices 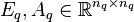 ,
, 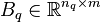 ,
, 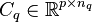 , where
, where 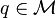 , correspond to the linear system active in mode
, correspond to the linear system active in mode 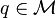 , and
, and 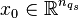 .
Here,
.
Here, 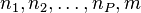 and
and  are positive integers and
are positive integers and 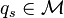 is the mode in which the system is
initialized.
We consider the
is the mode in which the system is
initialized.
We consider the 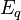 matrices to be invertible and
matrices to be invertible and 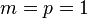 .
Furthermore, the transition from one mode to another is made via the so called switching or coupling matrices
.
Furthermore, the transition from one mode to another is made via the so called switching or coupling matrices 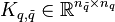 , where
, where 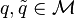 , as
, as 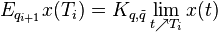 .
.
The restriction of the switching signal 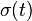 to a finite interval of time
to a finite interval of time ![[0,T]](/morwiki/images/math/b/7/4/b74093923941d33ee19becc5f4b48b25.png) is given as
is given as
where 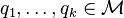 and
and 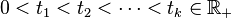 ,
, 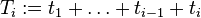 ,
, 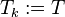 .
The input-output mapping is characterized in frequency domain by a series of multivariate rational functions obtained by computing the Laplace transform of generalized time kernels:
.
The input-output mapping is characterized in frequency domain by a series of multivariate rational functions obtained by computing the Laplace transform of generalized time kernels:
In general, we can write the level 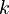 generalized transfer function associated to the switching sequence
generalized transfer function associated to the switching sequence 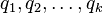 ,
and evaluated at the points
,
and evaluated at the points 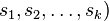 in the complex plane, as
in the complex plane, as
By using samples of such functions, we can directly construct (reduced) switched models that interpolate the original model, i.e. the extension of the Loewner framework to LSS.
For example, given a system 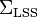 as in (17) with
as in (17) with 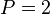 modes, consider the ordered tuples of left interpolation points:
modes, consider the ordered tuples of left interpolation points: 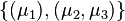 ,
, 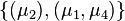 and right interpolation points
and right interpolation points 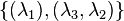 ,
, 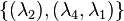 .
The projected Loewner matrices can be written as
.
The projected Loewner matrices can be written as
Then explicitly write the matrices 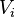 ,
, 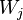 and
and 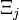 matrices (for
matrices (for 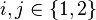 ) as
) as
where 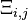 represent the reduced coupling matrices
represent the reduced coupling matrices 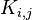 .
It follows that a reduced LSS of order
.
It follows that a reduced LSS of order 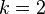 , denoted with
, denoted with 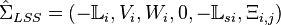 ,
, 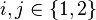 , can be obtained without computation matrix factorizations or solves.
This reduced system matches
, can be obtained without computation matrix factorizations or solves.
This reduced system matches 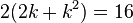 moments of the original system, namely:
moments of the original system, namely:
Summary
In this note we have addressed the Loewner framework for model reduction of some classes of (nonlinear) dynamical systems. The underlying philosophy valid for each of the extensions is as follows: One needs to collect data, i.e. values of high-order transfer functions (either by performing measurements or by direct numerical simulations) and then extract the desired information directly from the model constructed. The strength of the proposed approaches consists in the fact that, given input-output data, one can construct with basically no computational cost, a model of the data in generalized state-space format.
Further Variants
Additionally, there are further variants of the Loewner framework for parametric systems [11], [12], singular systems [13] and based on time-domain data [14].
References
- ↑ B.D.O. Anderson, A.C. Antoulas. Rational interpolation and state variable realizations. Proceedings of the 29th IEEE Conference on Decision and Control: 1865--1870, 1990.
- ↑ 2.0 2.1 2.2 A.J. Mayo, A.C. Antoulas. A framework for the generalized realization problem. Linear Algebra and Its Applications 426(2--3): 634--662, 2007.
- ↑ 3.0 3.1 A.C. Antoulas, S. Lefteriu, A.C. Ionita. A tutorial introduction to the Loewner Framework for model reduction. In: Model Reduction and Approximation for Complex Systems: 335--376, SIAM, 2017.
- ↑ A.C. Antoulas, I.V. Gosea, A.C. Ionita. Model reduction of bilinear systems in the Loewner framework. SIAM J. Sci. Comput. 38(5): B889--B916, 2016.
- ↑ 5.0 5.1 I.V. Gosea, A.C. Antoulas. Data-driven model order reduction of quadratic-bilinear systems. Numercial Linear Algebra with Applications: Accepted, 2018.
- ↑ I.V. Gosea, M. Petreczky, A.C. Antoulas. Model reduction of bilinear systems in the Loewner framework. SIAM J. Sci. Comput. 40(2): B572--B610, 2018.
- ↑ I.V. Gosea. Model order reduction of linear and nonlinear systems in the Loewner framework. Ph.D. thesis, Jacobs University Bremen, 2017.
- ↑ T. Carleman. Application de la théorie des équations intégrales linéaires aux systèmes d'équations différentielles non linéaires. Acta Math. 59: 63--87, 1932.
- ↑ G.P. McCormick. Computability of global solutions to factorable nonconvex programs: Part I -- Convex underestimating problems. Mathematical Programming 10(1): 147--175, 1976.
- ↑ A.C. Antoulas. The Loewner framework and transfer functions of singular/rectangular systems. Applied Mathematics Letters 54: 36--47, 2016.
- ↑ A.C. Antoulas, A.C.Ionita, S.Lefteriu. On two-variable rational interpolation. Linear Algebra and its Applications 436(8): 2889--2915, 2012.
- ↑ A.C. Ionita, A.C. Antoulas. Data-Driven Parametrized Model Reduction in the Loewner Framework. SIAM J. Sci. Comput. 36(3): A984--A1007, 2014.
- ↑ A.C. Antoulas. The Loewner framework and transfer functions of singular/rectangular systems. Applied Mathematics Letters 54: 36--47, 2016.
- ↑ B. Peherstorfer, S. Gugercin, and K. Willcox Data-Driven Reduced Model Construction with Time-Domain Loewner Models. SIAM J. Sci. Comput. 39(5): A2152--A2178,2017.

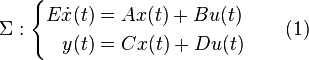
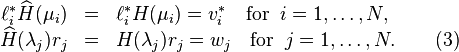
![\begin{array}{rcl}
M &=& \operatorname{diag}([\mu_1,\mu_2,\dots,\mu_N]) \in \mathbb{C}^{N \times N}, \quad \Lambda = \operatorname{diag}([\lambda_1,\lambda_2,\dots,\lambda_N]) \in \mathbb{C}^{N \times N}, \\
L^* &=& [\ell_1 \; \ell_2 \; \dots \; \ell_N] \in \mathbb{C}^{p \times N}, \quad R = [r_1 \; r_2 \; \dots \; r_N] \in \mathbb{C}^{m \times N}, \\
V^* &=& [v_1 \; v_2 \; \dots \; v_N] \in \mathbb{C}^{m \times N}, \quad W = [w_1 \; w_2 \; \dots \; w_N] \in \mathbb{C}^{p \times N}.
\end{array} \quad(4)](/morwiki/images/math/9/c/d/9cd97a579fba6e191a95918d58899d7f.png)