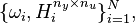Description
Motivation
Flexible aircraft models are very challenging in civil aeronautics due to their light-weight structure. Models are largely used by engineers to optimize and analyze critical phenomena in the pre-design phase. Such models can be used to monitor some dimensioning critical stress of the aircraft in response to discrete and continuous gust situations.
Computing responses to discrete gusts are expensive steps when designing and optimizing a new aircraft structure and geometry. In fact, this is part of the imposed clearance certifications requested by the flight authorities. During the aircraft preliminary design phase, this clearance is done by intensive simulations. However, due to the involved model's complexity, these latter are time-consuming and imply an important computational burden. Moreover, these simulations are involved at different steps of the aircraft optimization process, by aeroelastic, flight and control engineers.
In [1], a systematic way to fasten the gust simulation step and simplify the analysis by mean of data-driven model approximation in the Loewner framework is proposed, as well as a description of this model.
Considered data
This benchmark contains a set of frequency-domain input-output data computed from a high fidelity simulator, and given as the couple
where 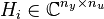 represents the transfer from
represents the transfer from 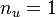 input signal (gust disturbance) to
input signal (gust disturbance) to 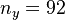 measurement outputs (accelerations and moments at different coordinates of a flexible aircraft wings and tail), evaluated at varying frequencies
measurement outputs (accelerations and moments at different coordinates of a flexible aircraft wings and tail), evaluated at varying frequencies 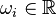 [rad/s], for
[rad/s], for 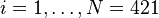 .
Specifically, the frequencies are between 0.1Hz until 42.1Hz in steps of 0.1Hz.
.
Specifically, the frequencies are between 0.1Hz until 42.1Hz in steps of 0.1Hz.
Origin
Collaboration between ONERA and DLR. The data from the high fidelity simulator have been generated by D. Quero (DLR), and the treatment performed jointly with P. Vuillemin, D. Quero and C. Poussot-Vassal.
Data
Description
The FlexibleAircraft.zip (1.4MB) repository contains three files:
- The dataONERA_FlexibleAircraft.mat data file, with
- W : the frequency values in rad/s (real
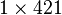 vector).
vector). - H : transfer function matrix evaluation at different output measurements points of the aircraft (complex
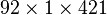 matrix).
matrix).
- W : the frequency values in rad/s (real
- The dataONERA_FlexibleAircraft_withMOR.mat data file, with 3 ROMs obtained with the MOR toolbox using the Loewner method
- Hr1 : linear rational ROMs with varying dimensions (state-space models in Matlab form).
- Hr2 : linear rational ROMs with varying dimensions, with stability post enforcement and input/output normalisation to catch all transfer whatever the amplitude (state-space models in Matlab form).
- The startONERA_FlexibleAircraft.m script file, used to loads and plots the data for illustration.
The transfer function matrix represents the transfer from the gust input to the 92 measurements gathering from
- 1--44: the local aerodynamic lift on the aerodynamic strips.
- 45--88: the local aerodynamic pitch moment on the aerodynamic strips.
- 89--92: the four generalized coordinates derivative (heave and pitch derivatives) and the first two flexible modes.
Objective
Find a (linear) stable reduced order model that well approximates the data.
Citation
To cite this benchmark, use the following references:
- For the benchmark itself and its data:
- The MORwiki Community, Flexible Aircraft. MORwiki - Model Order Reduction Wiki, 2018. https://morwiki.mpi-magdeburg.mpg.de/morwiki/index.php/Flexible_Aircraft
- For the background on the benchmark:
@inproceedings{PoussotMATHMOD:2018,
author = {C. Poussot-Vassal and D. Quero and P. Vuillemin},
title = {Data-driven approximation of a high fidelity gust-oriented flexible aircraft dynamical model},
booktitle = {IFAC PaperOnLine (9th Vienna International Conference on Mathematical Modelling)},
volume = {51},
year = {2018},
pages = {559--564},
doi = {10.1016/j.ifacol.2018.03.094}
}
References
- ↑ C. Poussot-Vassal, D. Quero, and P. Vuillemin, "Data-driven approximation of a high fidelity gust-oriented flexible aircraft dynamical model", in Proceedings of the 9th Vienna International Conference on Mathematical Modelling (MATHMOD), Vienna, Austria, 2018, pp 559--564.

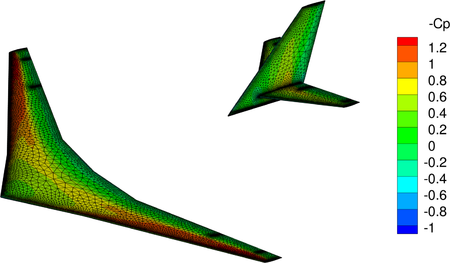
 of the aerostructure of the flexible aircraft.
of the aerostructure of the flexible aircraft.