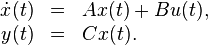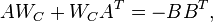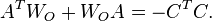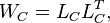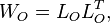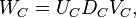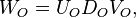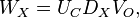Dominant Subspaces

Dominant Subspace Projection Model Reduction Method

The Dominant Subspace Projection Model Reduction Method (DSPMR), introduced in , or short Dominant Subspaces method is closely related to Balanced Truncation, and can be seen as a simplification. This is projection-based method is designed for linear time-invariant systems:

$\begin{array}{rcl} \dot{x}(t) &=& Ax(t) + Bu(t), \\ y(t) &=& Cx(t). \end{array}$

Similar to Balanced Truncation, the controllability Gramian matrix 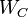$W_C$ and the observability Gramian matrix 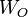$W_O$ are computed:

$AW_C+W_CA^T=-BB^T,$

$A^TW_O+W_OA=-C^TC.$

As a second step, instead of balancing controllability and observability subspaces, the respective subspaces are conjoined. Typically, (low-rank) Cholesky factors of the system Gramians are computed directly,

$W_C = L_C L_C^T,$

$W_O = L_O L_O^T,$

which are then combined using a singular value decomposition of the concatenated factors:

$[L_C, L_O] = U D V$.

The principal left (or right) singular vectors, based on the magnitude of the singular values, then serve as a Galerkin projection.

Alternatively, different approaches for the combination of subspaces can be used. For example in and , the singular vectors of the singular value decompositions of the system Gramians,

$W_C = U_C D_C V_C,$

$W_O = U_O D_O V_O,$

are concatenated and orthogonalized by a rank-revealing QR decomposition:

$[U_C, U_O] = Q R$,

with $Q$ being the resulting Galerkin projection.

Furthermore, the singular vectors of the system Gramians can also be combined by a second singular value decomposition as in .

Variants

Refined DSPMR

In , a variant called Refined Dominant Subspace Projection Model Reduction Method is presented. For this variant the subspaces are weighted by their Frobenius norm before combination, so for example:

$\Big[\frac{1}{\|L_C\|_{\text{Fro}}} L_C, \frac{1}{\|L_O\|_{\text{Fro}}} L_O\Big] = U D V$.

$\Big[\frac{1}{\|U_C\|_{\text{Fro}}} U_C, \frac{1}{\|U_O\|_{\text{Fro}}} U_O\Big] = Q R$.

Cross-Gramian-Based DSPMR

Instead of using controllability and observability Gramians, also the cross Gramian 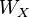$W_X$ can be used for the DSPMR procedure ,

$AW_X+W_XA=-BC,$.

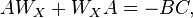The cross Gramian encodes controllability and observability, hence a singular value decompostion of the (the generally not-symmetric) cross Gramian matrix reveals dominant controllability and observability subspaces,

$W_X = U_C D_X V_O,$

which can then be combined by another singular value decomposition:

$[U_C, V_O] = U D V$.

The principal left (or right) singular values then represent the Galerkin projection.

This variant can also be refined, as proposed in , by scaling the left and right singular vectors by their associated singular values:

$[U_C D_X, V_O D_X] = U D V$.