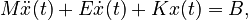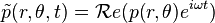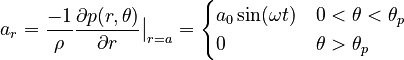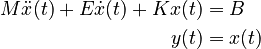| Background | |
|---|---|
| Benchmark ID |
circularPiston_n2025m1q2025 |
| Category |
oberwolfach |
| System-Class |
LTI-SOS |
| Parameters | |
| nstates |
2025
|
| ninputs |
1 |
| noutputs |
2025 |
| nparameters |
0 |
| components |
B, C, E, K, M |
| Copyright | |
| License |
NA |
| Creator | |
| Editor | |
| Location | |
|
NA | |
Description: Axi-Symmetric Infinite Element Model for Circular Piston
This example is a model of the form
with  ,
,  , and
, and 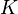 non-symmetric matrices and
non-symmetric matrices and  singular.
This is thus a differential algebraic equation.
It is shown that it has index 1[1].
The input of the system is
singular.
This is thus a differential algebraic equation.
It is shown that it has index 1[1].
The input of the system is  and the output is the state vector
and the output is the state vector  .
The motivation for using model reduction for this type of problem is the reduction of the computation time of a simulation.
.
The motivation for using model reduction for this type of problem is the reduction of the computation time of a simulation.
This is an example from an acoustic radiation problem discussed in [2].
Consider a circular piston subtending a polar angle 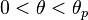 on a submerged massless and rigid sphere of radius
on a submerged massless and rigid sphere of radius 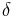 .
The piston vibrates harmonically with a uniform radial acceleration.
The surrounding acoustic domain is unbounded and is characterized by its density
.
The piston vibrates harmonically with a uniform radial acceleration.
The surrounding acoustic domain is unbounded and is characterized by its density  and sound speed
and sound speed  .
.
We denote by  and
and 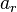 the prescribed pressure and normal acceleration respectively.
In order to have a steady state solution
the prescribed pressure and normal acceleration respectively.
In order to have a steady state solution 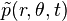 verifying
verifying
the transient boundary condition is chosen as:
The axi-symmetric discrete finite-infinite element model relies on a mesh of linear quadrangle finite elements for the inner domain
(region between spherical surfaces 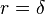 and
and 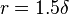 ).
The numbers of divisions along radial and circumferential directions are
).
The numbers of divisions along radial and circumferential directions are 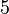 and
and 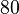 , respectively.
The outer domain relies on conjugated infinite elements of order
, respectively.
The outer domain relies on conjugated infinite elements of order 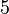 .
For this example we used
.
For this example we used ![\delta=1 [m]](/morwiki/images/math/9/8/b/98b34b28884957ce79f6b4bb2019cf84.png) ,
, ![\rho=1.225 [kg/m^3]](/morwiki/images/math/d/9/9/d9926e546d44cd98065096bdf2144ce5.png) ,
, ![c=340 [m/s]](/morwiki/images/math/2/9/f/29f4ae66a34fa19a680ca54b51bb76b1.png) ,
, ![a_0 = 0.001 [m/s^2]](/morwiki/images/math/d/8/9/d89f113e2ab68137e85ce3390d394592.png) and
and ![\omega = 1000 [rad/s]](/morwiki/images/math/e/1/f/e1f973f8ad2e6385b83034e3249f108d.png) .
.
The matrices 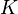 ,
,  ,
,  and the right-hand side
and the right-hand side 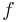 are computed by Free Field Technologies.
The dimension of the second-order system is
are computed by Free Field Technologies.
The dimension of the second-order system is 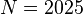 .
.
Origin
This benchmark is part of the Oberwolfach Benchmark Collection[3]; No. 38890, see [4].
Data
Download matrices in the Matrix Market format CircularPiston-dim1e3-piston.tar.gz (1.9 MB).
Extracting will produce
- piston.M
- piston.E
- piston.K
- piston.B
Note that for piston.B, loading with scipy.io.mmread will not work because the number of nonzeros is specified in the dense Matrix Market format. Replacing the line with "2025 1 2025" by "2025 1" will make it work.
Dimensions
System structure:
System dimensions:
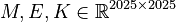 ,
,
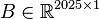 .
.
Citation
To cite this benchmark, use the following references:
- For the benchmark itself and its data:
- The MORwiki Community, Circular Piston. MORwiki - Model Order Reduction Wiki, 2018. http://modelreduction.org/index.php/Circular_Piston
@MISC{morwiki_piston,
author = {{The MORwiki Community}},
title = {Circular Piston},
howpublished = {{MORwiki} -- Model Order Reduction Wiki},
url = {https://modelreduction.org/morwiki/Circular_Piston},
year = {20XX}
}
- For the background on the benchmark:
@ARTICLE{PinA91,
author = {P.M. Pinsky and N.N. Abboud},
title = {Finite element solution of the transient exterior structural acoustics problem based on the use of radially asymptotic boundary conditions},
journal = {Computer Methods in Applied Mechanics and Engineering},
volume = {85},
pages = {311--348},
year = {1991},
doi = {10.1016/0045-7825(91)90101-B}
}
References
- ↑ J.-P. Coyette, K. Meerbergen, M. Robbé, Time integration for spherical acoustic finite-infinite element models, Numerical Methods in Engineering 64(13): 1752--1768, 2003.
- ↑ P.M. Pinsky and N.N. Abboud, Finite element solution of the transient exterior structural acoustics problem based on the use of radially asymptotic boundary conditions, Computer Methods in Applied Mechanics and Engineering, 85: 311--348, 1991.
- ↑ J.G. Korvink, E.B. Rudnyi, Oberwolfach Benchmark Collection, In: Dimension Reduction of Large-Scale Systems, Lecture Notes in Computational Science and Engineering, vol 45: 311--315, 2005.
- ↑ Z. Bai, K. Meerbergen, Y. Su, Second Order Models: Linear-Drive Multi-Mode Resonator and Axi Symmetric Model of a Circular Piston. In: Dimension Reduction of Large-Scale Systems. Lecture Notes in Computational Science and Engineering, vol 45: 363--365, 2005.