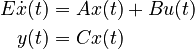RCL Circuit Equations

RCL Circuit Equations

Background
Benchmark ID	rclCircuitEquations_n1841m16q16 rclCircuitEquations_n306m2q2
Category	oberwolfach
System-Class	LTI-FOS
Parameters
nstates	1841 306
ninputs	16 2
noutputs	16 2
nparameters	0
components	A, B, C, E
Copyright
License	NA
Creator	Christian Himpe
Editor	Christian Himpe
Location
NA

Description

These benchmark originate from VLSI circuits. Specifically resistor-capacitor-inductor circuits, which can be represented by first order descriptor systems, following a modeling process based on the two Kirchhoff's circuit laws and the branch constitutive relations.

PEEC Problem

This RCL circuit is a PEEC discretization and has 2100 capacitors, 172 inductors, 6990 inductive couplings, as well as a resistive source,. The resulting model has 306 states, and two inputs and outputs.

Package Problem

The second problem models a 64-pin package of an RF circuit. A subset of eight pins carry signals, which leads to sixteen terminals (eight interior and eight exterior),. The resulting model has 1841 states, and sixteen inputs and outputs.

Origin

This benchmark is part of the Oberwolfach Benchmark Collection; see .

Data

The PEEC problem and package problem are available as MATLAB .mat files, providing the $A$, $B$, $E$ matrices, while 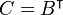$C = B^\intercal$ is assumed:

• PEEC.zip (32.8KB)
• Package.zip (78.7KB)

Dimensions

System structure:

$\begin{align} E \dot{x}(t) &= Ax(t) + Bu(t) \\ y(t) &= Cx(t) \end{align}$

System dimensions:

$E \in \mathbb{R}^{N \times N}$, $A \in \mathbb{R}^{N \times N}$, $B \in \mathbb{R}^{N \times M}$, $C \in \mathbb{R}^{M \times N}$.

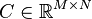System variants:

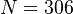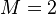$N = 306$, $M = 2$, for the PEEC problem, and 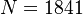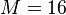$N = 1841$, $M = 16$ for the package problem.

Citation

To cite this benchmark, use the following references:

• For the benchmark itself and its data:

The MORwiki Community, RCL Circuit Equations. MORwiki - Model Order Reduction Wiki, 2019. http://modelreduction.org/index.php/RCL_Circuit_Equations

@MISC{morwiki_convection,
  author =       {{The MORwiki Community}},
  title =        {RCL Circuit Equations},
  howpublished = {{MORwiki} -- Model Order Reduction Wiki},
  url =          {https://modelreduction.org/morwiki/RCL_Circuit_Equations},
  year =         {20XX}
}

• For the background on the benchmark:

@INCOLLECTION{morFre05,
  author =       {R.W. Freund},
  title =        {RCL Circuit Equations},
  booktitle =    {Dimension Reduction of Large-Scale Systems},
  pages =        {367--371),
  year =         {2005},
  doi =          {10.1007/3-540-27909-1_22}
}